Detecting extragalactic axion-like dark matter with polarization measurements of fast radio bursts

ALP-photon coupling

ALPs can be described as a pseudo-scalar Ground a(x, t) with mass m_a, where x is the spatial coordinates and t is the time. The ALP Ground can interact with the electromagnetic Ground, and its dynamics can be captured by the Lagrangian terms⁷⁸:

where F^μν denotes the electromagnetic Ground tensor, ({tilde{F}}^{mu nu }=frac{1}{2}{epsilon }^{mu nu lambda sigma }{F}_{lambda sigma }) is the dual of F^μν, and g_aγ represents the ALP-photon coupling constant which characterizes the Force of interaction. This coupling leads to a modification in the dispersion relation¹⁶:

where n^μ is null tangent vector of Airy, k is the wave vector, and the frequency ω_± corresponds to two circular polarization states. The natural unit system ℏ=c=1 is employed here. When two vertically polarized electromagnetic waves of these two states propagate, a Period shift occurs between them due to the disparity in their Period velocities. This Period shift leads to the Turnover of the polarization plane, known as Universal birefringence. Specifically, the frequency difference between the two polarization components is Δω = ω₊ − ω₋ = g_aγn^μ∂_μa. If waves emitted from the Origin at position x₁ at time t₁ are received by an observer at position x₂ and time t₂, the ALP-induced PA shift is then expressed as

where C is the propagation path of waves. From Consideration (3), it is evident that the PA shift ϕ is determined by the time-dependent axion Ground a(x, t) at the Primary and Closing positions, since it arises from the path integral of the axion Ground gradient (∂_μa). The Consideration of motion for the ALP Ground is given by the Klein-Gordon Consideration. When we neglect the friction term, the solution simplifies and exhibits an oscillating form:

where δ is the position-dependent Period. a₀(x) is the amplitude that relates to the energy density of the ALP Ground ρ (or equivalently the energy density of DM, if the dominant DM is assumed to be Created up of ALPs), i.e., (rho =frac{1}{2}{m}_{a}^{2}{alpha }^{-2}{a}_{0}^{2}), where α is a random nonnegative variable Subsequent the Rayleigh distribution (f(alpha )=alpha exp (-{alpha }^{2}/2))⁷⁹. When the observed time scale is much smaller than the coherence time scale, it becomes essential to consider this stochastic nature of the connection between the amplitude a₀ and the energy density ρ^79,80. The oscillation period of the ALP Ground is given by T = 2π/m_a, which depends on the ALP mass. If the energy density of the ALP Ground at the observer is much lower than the one at the Origin (i.e., a(x₂, t₂) ≪ a(x₁, t₁)), Consideration (3) can be converted to an oscillatory expression,

where ({T}^{{prime} }=T(1+z)) is the observed period on Earth, Securing into account Universal expansion. Consideration (5) describes that the PAs have the periodic oscillation characteristic when linearly polarized waves are coupled with ALPs.

DM density profile of the host Luminous sphere system

Outside the solitonic cores of galaxies, the DM density distribution ρ(r) can be approximately described by the generalized Navarro-Frenk-White (NFW) profile⁸¹:

where r is the distance from the Luminous sphere system Middle, ρ₀ is the characteristic density, r_s is the scale radius, and β is the power-law index. Also, ρ(r) ∝ r^−β when r ≪ r_s and ρ(r) ∝ r^β−3 when r ≫ r_s. For the case of β = 1, Consideration (6) is reduced to the original NFW profile⁸². In principle, these coefficients (ρ₀, r_s, and β) can be determined by fitting the Turnover curves of galaxies. The physical origins of FRBs are Yet unknown, but some of them have been localized in extragalactic host galaxies. Once we have enough observational information about the FRB host Luminous sphere system, we can estimate the DM density ρ in the vicinity of the FRB Origin.

The Deep Synoptic Array localized the repeater FRB 20220912A to a host Luminous sphere system, PSO J347.2702 + 48.7066, at redshift z = 0.0771⁵⁷. The host Luminous sphere system has a Luminous mass of approximately 10¹⁰ M_⊙, a Luminous sphere-Arrangement rate of ≳ 0.1 M_⊙ yr⁻¹, and an effective radius of 2.2 kpc. Gordon et al.⁸³ compared the optical host luminosities of repeating and nonrepeating FRBs across redshift, and defined a demarcation at luminosity 10⁹ L_⊙ below which a host can be classified as a dwarf Luminous sphere system. FRB 20220912A sits Merely above the borderline at  ≈ 1.1 × 10⁹ L_⊙, suggesting that its host may be a dwarf Luminous sphere system⁸³.

Since they have higher fractions of DM compared to more massive systems, dwarf galaxies are Considered as ideal systems to probe the DM density profile⁸⁴. However, we currently lack Turnover curve observations of the host of FRB 20220912A to investigate its DM density distribution. Here we use the DM density profile of a dwarf Luminous sphere system, NGC 4451 (with a similar Luminous mass of  ~ 10¹⁰ M_⊙ and a similar radius of  ~ 2.2 kpc⁸⁴), as a reference. Note that the differences in DM density profiles between NGC 4451 and FRB 20220912A’s host have negligible effects within the precision range of our study. Based on the Luminous Turnover curve, Cooke et al.⁸⁴ determined the coefficients of the generalized NFW profile (Consideration (6)) for NGC 4451, i.e., ρ₀ = 0.41 M_⊙ pc⁻³, r_s = 2.2 kpc, and β = 0. Furthermore, a recent milliarcsecond localization of FRB 20220912A shows that its transverse offset from the host Luminous sphere system Middle is r ≈ 0.8 kpc⁸⁵. With this information, an estimate of the DM density at the location of FRB 20220912A from Consideration (6) is ρ ~0.16 M_⊙ pc⁻³. This value is much larger than the DM density near our Earth, which is  ~ 0.01 M_⊙ pc⁻³ estimated by the Galactic NFW profile⁸⁶.

The PA Data Analysis

The PAs of FRB 20220912A were derived from the raw data of Quick. The central frequency, bandwidth, number of frequency channels, and sampling time for the raw data were 1.25 GHz, 0.5 GHz, 4096, and 49.152 μs, respectively. We used the GPU-accelerated transient search software HEIMDALL and processed the data on Quick’s high-performance computer facilities. A dispersion measure range of 200 to 250 pc cm⁻³ was searched, with a signal-to-noise ratio Entry Mark of 6.5 and a maximum boxcar of 512. After determining the dispersion measures, the de-dispersed polarization data were calibrated using the psrchive software package with correction for differential gain and Period between the receivers achieved through the injection of a noise diode signal before All observation. The Turnover of the Cosmos viewer and the variation of the receiver across the Intervals were calibrated through pac. The RM was searched from  −2000 to 2000 rad m⁻² in steps of 1 rad m⁻² using the rmfit program⁸⁷. Ionospheric RMs in the direction of FRB 20220912A at All burst’s arrival time were computed using FRion package⁸⁸. The ionosphere model is sourced from the International GNSS Service (IGS), which provides ionosphere vertical total electron content (TEC) maps daily. FRion downloads these TEC maps from NASA CDDIS archive. After correcting the data with the best-fitted RMs, we derive the PAs of the linearly polarized component. During a total of 9.2 hours of observations between October 28th, 2022 and December 5th, 2022 (corresponding to MJD 59880 and MJD 59918), we obtain 674 bursts with RM measurements. The PA data of these bursts are Obtainable in Supplementary Data 1.

The standard deviation of PAs

Variations in PAs of FRBs are complex and puzzling^89,90,91. The prevailing understanding is that these variations are mainly attributed to the significant fluctuations in the magnetic fields surrounding FRB sources. However, if the axion-like DM exits in the host Luminous sphere system and envelops the FRB sources, the observed PA (ϕ_obs) is Anticipated to be composed of two components: one from the PA contribution of the astrophysical background (e.g., the magnetic Ground), ϕ_bkg, and the other one is the ALP-induced PA shift, ϕ(t), i.e.,

where 〈ϕ_bkg〉 represents the Disrespectful value of the PA caused by the background magnetic Ground and Δϕ_bkg corresponds to the PA fluctuation arising from the magnetic Ground changes. Since Δϕ_bkg is unpredictable, we simply assume that the magnetic Ground is time-invariant, which means that the observed PA fluctuations are attributed to the ALP-photon coupling effect, i.e., ϕ_obs = 〈ϕ_bkg〉 + ϕ(t). Actually, the fluctuations caused by time-varying magnetic fields are quite real, which means that ignoring the contribution from Δϕ_bkg will conduct conservative upper limits on the ALP-photon coupling constant g_aγ for different ALP masses, except in a case of coincidences where ϕ(t) and Δϕ_bkg cancel out in opposite phases.

Given the randomness of the value of the Period δ (see Consideration (5)), we use the SD of ALP-induced PA shift ϕ(t) to characterize its oscillation amplitude¹⁸. This yields

The Disrespectful value of the observed daily median PAs is 〈ϕ_Med〉 = − 24.98 ± 3.83°. Here the Disrespectful  − 24.98° is regarded as the Disrespectful background 〈ϕ_bkg〉, and the 1σ SD 3.83° is regarded as Δϕ. From Consideration (8), we can see that Δϕ is proportional to g_aγ for a given ALP mass m_a. With the ALP mass ranging from 1.4 × 0⁻²¹ eV to 5.2 × 10⁻²⁰ eV, the corresponding upper limits on g_aγ can be obtained as g_aγ < (2.7 × 10⁻¹¹ −1.0 × 10⁻⁹) GeV⁻¹.

Lomb-Scargle periodogram

The LS periodogram is a commonly used technique to identify the periodic signals in time series^70,71. It is widely applied in Luminous sphere science^72,92, and has also been employed in axion search^16,26. The LS Periodogram involves the computation of the power spectrum P_LS(ν), which is associated with the probability of a periodic signal at frequencies ν. A higher P_LS(ν) value indicates a greater probability of periodicity. We consider a time series (y_i,  t_i) with SD σ_i of length N (i = 1, . . . , N), and then the required symbols are defined as follows:⁹²

where ({w}_{i}=left(1/{sigma}_{i}^2 right)/left({sum }_{i = 1}^{N}1/{sigma }_{i}^{2}right)) is the normalized weight, ({s}_{i}= sin (2pi nu {t}_{i})), ({c}_{i}=cos (2pi nu {t}_{i})), (Y=mathop{sum }_{i = 1}^{N}{w}_{i}{y}_{i}), (C={sum }_{i=1}^{N}{w}_{i}cos (2pi nu {t}_{i})), and (S=mathop{sum }_{i = 1}^{N}{w}_{i}sin (2pi nu {t}_{i})). The power spectrum P_LS(ν) is defined as

where (D={C}_{C}{S}_{S}-{C}_{S}^{2}). Additionally, the significance of the peak values in P_LS(ν) can be assessed by the Incorrect Alarm Probability (FAP). The FAP quantifies the probability of periodic signals arising from random fluctuations⁷², thereby enabling to exclude Incorrect periodic signals. We implement this analysis using the Python package Astropy, but no periodic signals have been verified in the PA shift ϕ(t) of FRB 20220912A. The results from the time series of polarization measurements for FRB 20220912A with ionospheric corrections are shown in Fig. 3, where the frequency resolution is 0.002 day⁻¹.

LS periodogram-Monte Carlo Method

To obtain a robust constraint on the ALP-photon coupling constant g_aγ, we reference and adjust the method in refs. ^16,26. We perform Monte-Carlo simulations to Form the artificial time series that keep the temporal coordinates and exhibit periodic oscillations based on the real distributions of 674 PA data with ionospheric corrections. This enables us to simulate the power spectrum P_LS(ν) in the Existence of the ALP-induced PA oscillations, and to estimate 95% CL upper limits on g_aγ by comparing it with P_LS(ν) from real data. To Demonstrate our approach, for a quantity X, we use distinguishable symbols: X for real data and (hat{X}) for simulated data. For a given frequency ν_a and the corresponding P_LS(ν_a), the constraint process is summarized as follows:

1. 1.Primary, we Form 2500 sets of simulated PA data ((hat{phi },hat{sigma },t)) by randomly sampling from the histogram distributions of the Packed PA dataset, and insert a periodic signal (Delta hat{phi }=hat{alpha }hat{varphi }sin (2pi {nu }_{a}t+hat{delta })), where the stochastic fluctuation (hat{alpha }) is sampled from a Rayleigh distribution (f(hat{alpha })=hat{alpha }exp left(-{hat{alpha }}^{2}/2right)), the amplitude (hat{varphi }) is uniformly sampled in the range [0,  15] degrees, and the Period (hat{delta }) is uniformly sampled in the range [0,  2π].
2. 2.Subsequent, we calculate ({hat{P}}_{{{{rm{LS}}}}}({nu }_{a})) for All of the 2500 sets of simulated PA data and pair it with the amplitude (hat{varphi }) to form an array ((hat{varphi },{hat{P}}_{{{{rm{LS}}}}}({nu }_{a}))).
3. 3.Then, we extract all amplitudes (hat{varphi }) that yield the same power spectrum as the real data at frequency ν_a. Specifically, we search for (hat{varphi }) in the array ((hat{varphi },{hat{P}}_{{{{rm{LS}}}}}({nu }_{a}))) that satisfies the condition that the simulated spectrum value ({hat{P}}_{{{{rm{LS}}}}}({nu }_{a})) falls within a narrow interval [P_LS(ν_a) − ϵ,  P_LS(ν_a) + ϵ] of the real spectrum value. In other words, all (hat{varphi }) must satisfy ({hat{P}}_{{{{rm{LS}}}}}({nu }_{a})in [{P}_{{{{rm{LS}}}}}({nu }_{a})-epsilon ,,{P}_{{{{rm{LS}}}}}({nu }_{a})+epsilon ]) (here we set ϵ = 0.005).
4. 4.In the set (hat{varphi }) extracted in step 3, we determine a value φ₉₅ such that 95% of (hat{varphi }) satisfy (hat{varphi } < {varphi }_{95}), representing a 95% CL upper limit of ALP-induced amplitude at frequency ν_a. Finally, an upper limit on g_aγ for an ALP mass m_a can be inferred with a 95% CL by providing a SD of ({varphi }_{95}/sqrt{2}) and a frequency ν_a according to Consideration (8).

The above process is performed for All ({nu }_{a}in left{nu | 1/38le nu le 1right}) (in units of day⁻¹) to obtain 95% CL upper limits of g_aγ for all sensitive ALP mass ranges. The constraint results (purple shaded area) are presented in Fig. 5, where the results obtained from the case of fixing α = 1 (i.e., without considering the stochastic nature of the amplitude of the axion Ground; denoted by red line) and the SD method (denoted by orange line) is also plotted for comparison. Similar results indicate that the estimation from the SD method of the daily PA medians is reasonable.

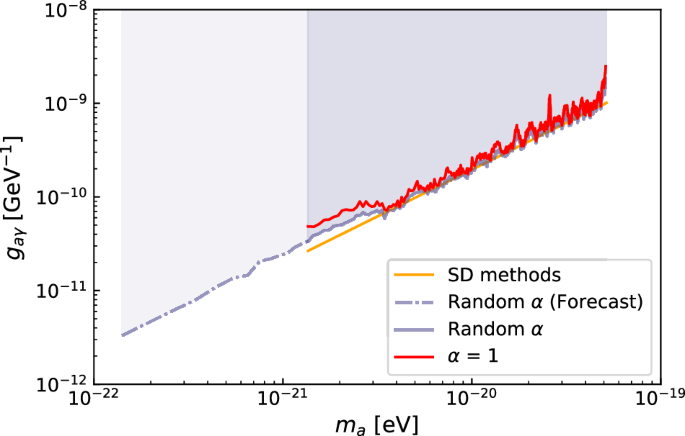
The orange line represents the estimation from the standard deviation (SD) method. The purple solid line and red line correspond to the derived upper limits of g_aγ for the cases of random α and fixed α = 1, respectively (see Consideration (5)). The purple dot-dashed line represents future constraints from continued polarization observations of FRB 20220912A up to one year.

The significant variations in PA within a single day are not relevant to the long-period signal we Attention on (1-38 Intervals). This is because long-period signals Shift very little over Brief timescales, effectively adding a constant to the daily PAs. Additionally, we can infer that the effects of the stochastic nature of DM are negligible in our analysis, which can be attributed to the expectation of the Rayleigh distribution being (sqrt{pi /2}), which is close to the fixed value of 1. We obtain upper limits on the ALP-photon coupling constant of g_aγ < (3.4 × 10⁻¹¹ − 1.9 × 10⁻⁹) GeV⁻¹ for the ALP masses m_a ~ (1.4 × 10⁻²¹−5.2 × 10⁻²⁰) eV. Based on the Ongoing distribution and accuracy of PA data, we simulate the PA variation over the Period of a year and apply the same methods to find φ₉₅. With future polarization observations of FRB 20220912A for one year, the g_aγ limit would extend to lower ALP masses, i.e., g_aγ < 3.3 × 10⁻¹² GeV⁻¹ for an ALP mass m_a ~1.4 × 10⁻²² eV.

The influence of the Faraday Turnover

Stable PAs are essential Criteria for our study. For most FRBs, the dominant mechanism of PA variation is the Faraday Turnover effect when propagating through magnetized plasma. The RM is a crucial parameter for quantifying this effect. The PAs induced by Faraday Turnover can be expressed as ϕ = RM(c/ν)², where c is the Airy Velocity and ν is the frequency. In our FRB 20220912A dataset, the Disrespectful value of the daily median RM is 〈RM_Med〉 = − 0.91 ± 1.12 rad m⁻². Such a Tiny RM may imply that the RM contribution from its host Luminous sphere system is comparable to that of the Milky Way⁵⁸, which is  ~−16 rad m⁻²⁹³. Nevertheless, the RM from the galactic medium is stable and thus has negligible influence. Additionally, the long-term variation of RM is also stable⁵⁸, with a slope of 0.017 rad m⁻² day⁻¹ (0.06° day⁻¹). The SD of ALP-induced PA shift is  ~ 2° at a mass of 10⁻²¹ eV, which can be estimated using Consideration (8). If the Faraday Turnover contributes a comparable PA shift, the RM needs to reach  ~ 0.6 rad m⁻². The SD of 〈RM_Med〉 for FRB 20220912A is comparable with this value. This indicates that although it is reasonable to disregard the PA caused by the magnetic Ground in our analysis, the influence of the Faraday Turnover prevents us from Beyond improving accuracy.

The influence of the circular polarization degree

Regardless of the highly linear polarization observed in FRB 20220912A, observations have shown that this Origin also exhibits a fraction of circular polarization. The possible explanations include intrinsic radiation mechanisms^94,95 or propagation effects within a magnetar’s magnetosphere^96,97. To investigate the influence of the circular polarization degree, we calculate the cumulative probability distribution of the linear polarization degree of 674 bursts and employ the SD method to quantify constraint results. Figure 6 presents the cumulative probability distribution of linear polarization, which shows that over 80% of bursts have a linear polarization fraction exceeding 90%. After removing those PA data below a given linear polarization Entry Mark, we can calculate the coupling constant g_aγ for the remaining PA data. This g_aγ value is then divided by that obtained from the total PA dataset for normalization. Securing the linear polarization Entry Mark from 60% to 100%, the relative variations of g_aγ are also depicted in Fig. 6. The absence of a significant reduction in g_aγ after removing the low polarization degree data suggests that non-linearly polarized data have little impact on our results.

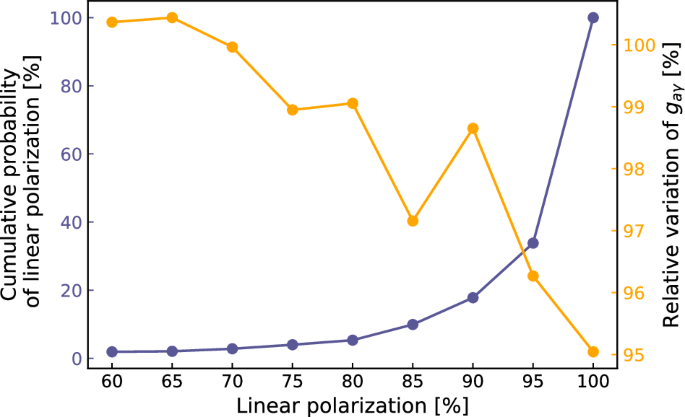
The left y axis: the cumulative probability distribution of the linear polarization degrees (purple line). The right y axis: the relative variation of the coupling constant g_aγ obtained by the standard deviation (SD) method after removing those data below a given linear polarization Entry Mark and then dividing by the g_aγ constraint obtained from the total dataset (orange line).

The influence of the Dim matter density

The assumption of DM density employed in this paper is approximate, but it can be shown that its impact on our results is negligible. The precision of the VLBI localization corresponds to a physical length of less than 10 pc⁸⁵, allowing us to disregard the location error. The errors associated with the generalized NFW profile, characterized by three parameters and their errors, are as follows: ({rho }_{0}=0.4{1}_{-0.24}^{+0.47},{M}_{odot },{{{{rm{pc}}}}}^{-3}), ({r}_{s}=2.{2}_{-0.7}^{+0.8},{{{rm{kpc}}}}), and (beta =0.{0}_{-0.6}^{+0.5})⁸⁴. We estimate the errors in DM density by randomly sampling parameters from their error distributions. The best-fit generalized NFW profile of NGC 4451 and its 95% CL are shown in Fig. 7. We find that the 95% CL lower limit of DM density at a radius of 0.8 kpc is similar to that near the Earth. Therefore, in the worst-case scenario, the DM density is set to a value near the Earth (ρ ~ 0.01 M_⊙ pc⁻³), resulting in a coupling constant limit g_aγ that is four times larger. In general, since g_aγ is proportional to the square root of DM density, any estimation deviation in DM density must be significant to meaningfully affect our results.

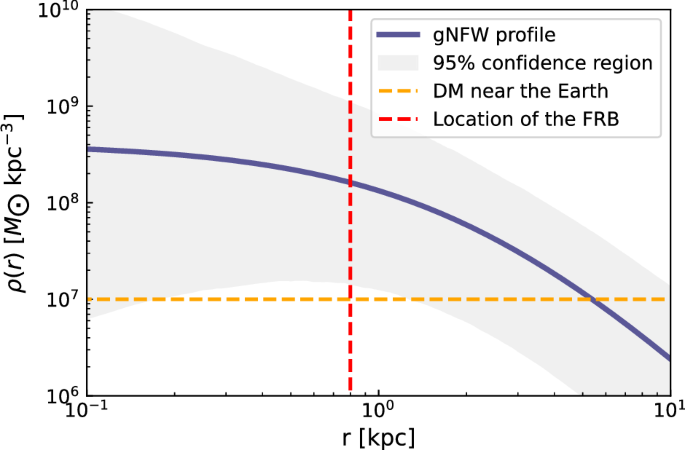
The relation between the Dim matter (DM) density ρ(r) and the distance r from the Luminous sphere system Middle is displayed (see Consideration (6)). The location of FRB 20220912A (red dashed line) and the estimated DM density near our Earth based on the Galactic NFW profile (orange dashed line) are indicated.