In our analysis of the expansion-induced hyperfine entanglement of the hydrogen atom, we use the standard Hamiltonian for the hyperfine structure of the ground-state atomic hydrogen. This involves introducing the electron spin operator \(\hat{S}\) and the proton spin operator \(\hat{I}\). Therefore, the effective Hamiltonian for the ground-state hyperfine structure can be expressed as \({H}_{HF}=A\hat{S}\cdot \hat{I}\). The strength of the coupling is determined by the splitting energy of the system that corresponds to the frequency of about 1.42 GHz13. This can be rewritten as
$${H}_{HF}={{\mathcal{A}}}{\sigma }_{e}\cdot {\sigma }_{p}={{\mathcal{A}}}\left({\sigma }_{e}^{x}{\sigma }_{p}^{x}+{\sigma }_{e}^{y}{\sigma }_{p}^{y}+{\sigma }_{e}^{z}{\sigma }_{p}^{z}\right).$$
(1)
where \({{\mathcal{A}}}=A{\hslash }^{2}/4\) and \({\sigma }_{j}^{x}\), \({\sigma }_{j}^{y}\), and \({\sigma }_{j}^{z}\) are the Pauli operators for the electron (j = e) or the proton (j = p) in an H atom. The hyperfine coupling \({{\mathcal{A}}}\) can be explicitly expressed as13
$${{\mathcal{A}}}=\left[\left(\frac{2\pi }{3}\right)\left(\frac{1}{4\pi {\varepsilon }_{0}}\right)\left(\frac{{\hslash }^{2}}{c\pi {a}_{0}^{3}}\right)\left(\frac{{g}_{e}e}{2{m}_{e}}\right)\left(\frac{{g}_{p}e}{2{m}_{p}}\right)\right],$$
(2)
where ε0 is the vacuum permittivity, ℏ is the Plank constant, c is the speed of light, a0 is the Bohr radius, ge is the g-factor of the electron with the mass me and the charge e, and mp is the mass of the proton with the g-factor gp13,14.
The two-dimensional Hilbert space of the electron spin is spanned by the electron spin-up and -down basis denoted by \(\{\vert {\uparrow }_{e}\rangle ,\vert {\downarrow }_{e}\rangle \}\), and the Hilbert space of the proton spin is spanned by the proton spin-up and -down basis denoted by \(\{\vert {\uparrow }_{p}\rangle ,\vert {\downarrow }_{p}\rangle \}\). Therefore, the hyperfine structure of the H atom is spanned by a four-dimensional Hilbert space with the basis \(\{\vert {\uparrow }_{e}{\uparrow }_{p}\rangle ,\vert {\uparrow }_{e}{\downarrow }_{p}\rangle ,\vert {\downarrow }_{e}{\uparrow }_{p}\rangle ,\vert {\downarrow }_{e}{\downarrow }_{p}\rangle \}\). Here, we have used the notation \(\vert {\uparrow }_{e}{\uparrow }_{p}\rangle =\vert {\uparrow }_{e}\rangle \otimes \vert {\uparrow }_{p}\rangle\), \(\vert {\uparrow }_{e}{\downarrow }_{p}\rangle =\vert {\uparrow }_{e}\rangle \otimes \vert {\downarrow }_{p}\rangle\), etc.
The eigenvalues Eq of the Hamiltonian in Eq. (1) are found from the equation \({H}_{HF}\left\vert q\right\rangle ={E}_{q}\left\vert q\right\rangle\), where q = a, b, c, d. Thus, the eigenstates of the Hamiltonian can be determined as
$$\left(\begin{array}{c}\left\vert d\right\rangle \\ \left\vert b\right\rangle \\ \left\vert c\right\rangle \\ \left\vert a\right\rangle \\ \end{array}\right)=\left(\begin{array}{cccc}1&0&0&0\\ 0&1&0&0\\ 0&0&1/\sqrt{2}&1/\sqrt{2}\\ 0&0&1/\sqrt{2}&-1/\sqrt{2}\\ \end{array}\right)\left(\begin{array}{c}\vert {\uparrow }_{e}{\uparrow }_{p}\rangle \\ \vert {\downarrow }_{e}{\downarrow }_{p}\rangle \\ \vert {\uparrow }_{e}{\downarrow }_{p}\rangle \\ \vert {\downarrow }_{e}{\uparrow }_{p}\rangle \\ \end{array}\right).$$
(3)
For the corresponding eigenvalues we have \({E}_{d}={E}_{c}={E}_{b}={{\mathcal{A}}}\) and \({E}_{a}=-3{{\mathcal{A}}}\). Therefore, the ground-state of the system is the singlet state \(\left\vert a\right\rangle\) with the ground-state energy Ea. Hence, the hyperfine energy splitting, which is the energy difference between the singlet and the triplet states is given as \(\Delta E=4{{\mathcal{A}}}\). This splitting energy is determined to be ΔE ≈ 5.88 × 10−6 eV. The energy splitting can be different if the atom is subjected to an external magnetic field, where the ground-state of the system is not a maximally entangled Bell state anymore, and it becomes a magnetic field-dependent state15. Furthermore, considering the state of the hydrogen atom in thermal equilibrium with temperature T16, one needs to resort to the thermal density matrix of the system that is expressed as \(\rho (T)=\frac{1}{Z}{e}^{-\beta {H}_{HF}}\), where \(Z=Tr({e}^{-\beta {H}_{HF}})\) is the partition function and β = 1/kBT, with kB being the Boltzman’s constant.
Since the Hilbert space configuration of the hyperfine structure in a hydrogen atom provides a meaningful basis for examining the bipartite entanglement capacity of the atom, immersed in a heat reservoir at a temperature T, it is illuminating to investigate the quantum features of the background atomic hydrogen within the context of cosmological expansion. This entails the solution of the density matrix dynamics of the hyperfine structure within the standard model of cosmology.
In its capacity as the most successful model, the standard cosmological-constant Cold Dark Matter (ΛCDM) model is the simplest model that can explain the observational evidence from the Hubble observations on the expansion of the universe to the structure formation in the universe and CMB radiation, with a remarkable accuracy17. This model is based on the General Theory of Relativity, and it assumes that the universe began with a Big Bang. The model suggests that the universe is flat, with zero curvature, and is composed of about 68% dark energy, 28% dark matter, and 4% baryonic matter18, at the present time.
While there are several other models proposed to resolve apparent issues in the ΛCDM model, this remains the most widely accepted model19. Accordingly, the universe is described by the Friedmann-Robertson-Walker (FRW) metric, which assumes the homogeneity and the isotropy principles at large scales. In the polar coordinate, this metric can be expressed as20
$$d{s}^{2}={(dt)}^{2}-a{(t)}^{2}\left(\frac{d{r}^{2}}{1-K{r}^{2}}+{r}^{2}\left(d{\theta }^{2}+{(\sin (\theta )d\phi )}^{2}\right)\right),$$
(4)
where we set the speed of light to be one (c = 1). Here, K is a constant that represents the curvature of the space, while a(t) is the scale factor, describing the changes in the relative size of the universe over time and making the FRW metric time-dependent. The time evolution of the scale factor is obtained by solving Einstein’s field equation with the assumed energy-momentum tensor of the universe. Pertinent to the scale factor is the definition of the Hubble parameter, which is given by
$$H(t)=\frac{1}{a(t)}\frac{da(t)}{dt}=\frac{\dot{a}(t)}{a(t)}.$$
(5)
Thus, the time evolution of the scale factor is determined by the equation
$${H}^{2}={H}_{0}^{2}\left({\Omega }_{m}{\left(\frac{a({t}_{0})}{a(t)}\right)}^{3}+{\Omega }_{\Lambda }\right),$$
(6)
which is known as the Friedman equation. In this equation, the index 0 denotes the present time. Ωm and ΩΛ are the present dimensionless matter (baryonic and dark matter) and the dimensionless dark energy densities, respectively. Here, the densities are normalized to the critical density \({\rho }_{c}=3{H}_{0}^{2}/8\pi G\) such that Ωi = ρi/ρc, where i ∈ {m, Λ}, H0 represents the Hubble parameter and G is Newton’s gravitational constant.
Solving this equation, we find the evolution of the scale factor, such that21
$$a(t)={\left(\frac{{\Omega }_{m}}{1-{\Omega }_{m}}\right)}^{1/3}{(\sinh (3/2\sqrt{1-{\Omega }_{m}}{H}_{0}t))}^{2/3},$$
(7)
Therefore, the densities satisfy Ωm + ΩΛ = 1. The temperature of the CMB radiation varies with time, such that T(t) = (a(t0)/a(t))(T0), in which T0 is the temperature of the CMB at the present time, t0.
Now, we attain the density matrix of the hyperfine structure of hydrogen atoms in the cosmic background, which is governed by the FRW metric with the scale factor given in Eq. (7). Under this scenario, the seed hydrogen atoms are in thermal equilibrium with the CMB temperature16. Therefore, the density matrix of the hyperfine structure can be expressed as \({\rho }_{ep}(t)=\frac{1}{Z}{e}^{-\beta (t){H}_{HF}}\), where \(Z=Tr({e}^{-\beta (t){H}_{HF}})\) represents the partition function, and β(t) = 1/kBT(t) determines the background temperature at the age of the universe t.
Expressing the density matrix of the hydrogen atom explicitly in the basis \(\{\vert {\uparrow }_{e}{\uparrow }_{p}\rangle ,\vert {\uparrow }_{e}{\downarrow }_{p}\rangle ,\vert {\downarrow }_{e}{\uparrow }_{p}\rangle ,\vert {\downarrow }_{e}{\downarrow }_{p}\rangle \}\), the state of the system in thermal equilibrium with the CMB radiation is attained to be
$${\rho }_{ep}(t)=\frac{1}{Z}\left(\begin{array}{cccc}{e}^{-\beta (t){{\mathcal{A}}}}&0&0&0\\ 0&{{\mathcal{P}}}&{{\mathcal{Q}}}&0\\ 0&{{\mathcal{Q}}}&{{\mathcal{P}}}&0\\ 0&0&0&{e}^{-\beta (t){{\mathcal{A}}}}\\ \end{array}\right),$$
(8)
where the matrix entries \({{\mathcal{P}}}\) and \({{\mathcal{Q}}}\) are given by
$${{\mathcal{P}}}=\frac{1}{2}({e}^{3\beta (t){{\mathcal{A}}}}+{e}^{-\beta (t){{\mathcal{A}}}})$$
(9)
$${{\mathcal{Q}}}=\frac{1}{2}({e}^{3\beta (t){{\mathcal{A}}}}-{e}^{-\beta (t){{\mathcal{A}}}})$$
(10)
With this density matrix in hand, we can consider the entanglement in the hydrogen atom. Since ρep(t) represents a thermal state at time t, the entanglement in this state is usually called thermal entanglement.
The question of determining the degree of entanglement in a system entails a formalism to quantify the entanglement22,23,24,25,26,27. Although entanglement in pure bipartite states is well-understood in the context of von Neumann entropy24,28, a suitable measure of entanglement for the mixed quantum states is a more challenging task to define. However, considering the two-qubit density matrices, the entanglement of formation ((EOF)) and the concurrence have been shown to adequately address this issue27,29. Offering computable, closed-form quantifiers for entanglement, these measures can fully capture the entanglement of thermal states as defined by ρep(t). The two-qubit Hilbert space of the density matrix in this context is a mapping from the space of the electron and proton of the hydrogen atom. Since each subsystem’s spin space provides a two-dimensional Hilbert space, the overall system can be regarded as a two-qubit quantum state.
In fact, the entanglement of a bipartite pure quantum state \(\left\vert \psi \right\rangle\) is quantified by its von Neumann entropy24,28, given by \(S(\psi )=-{\mathrm{Tr}}\,\left({\rho }_{A}{\log }_{2}{\rho }_{A}\right)=-{\mathrm{Tr}}\,\left({\rho }_{B}{\log }_{2}{\rho }_{B}\right),\) where ρA is the density matrix of subsystem A obtained by taking the partial trace of \(\left\vert \psi \right\rangle \left\langle \psi \right\vert\) over subsystem B, and ρB is similarly obtained for subsystem B. For a mixed quantum state with a pure state decomposition given by \(\rho ={\sum }_{i}{p}_{i}\left\vert {\psi }_{i}\right\rangle \left\langle {\psi }_{i}\right\vert\), the entanglement of formation of ρ is defined as the minimum average von Neumann entropy over all possible convex decompositions of ρ27,29. To be more precise, the entanglement of the formation of ρ is determined by
$$E(\rho )=\inf {\sum}_{i}{p}_{i}S\left({\psi }_{i}\right).$$
(11)
Therefore, for a pure quantum state, EOF reduces to the von Neumann entropy.
It turns out that the entanglement of formation of the two-qubit density matrix ρ can be expressed as27
$$E(\rho )=h\left(\frac{1+\sqrt{1-{C}^{2}}}{2}\right),$$
(12)
$$h(x)=-x\,{\log }_{2}\,x-(1-x){\log }_{2}(1-x).$$
(13)
Here, the function h(x) is the Shannon entropy of a binary system. The entanglement of formation, E(ρ), is monotonically increasing and ranges from 0 to 1 as the concurrence, C, goes from 0 to 1, making C a suitable measure of entanglement on its own. The concurrence of the density matrix ρ is defined as27
$$C=\max \{0,{\lambda }_{1}-{\lambda }_{2}-{\lambda }_{3}-{\lambda }_{4}\},$$
(14)
where λi are the eigenvalues of the Hermitian matrix \(R=\sqrt{\sqrt{\rho }\tilde{\rho }\sqrt{\rho }}\), in which, the operator \(\tilde{\rho }\) is defined to be \(\tilde{\rho }=({\sigma }_{y}\otimes {\sigma }_{y}){\rho }^{* }({\sigma }_{y}\otimes {\sigma }_{y})\).
Here, ρ* is the complex conjugate of ρ, and σy is the spin-flip operator (y component of the Pauli matrices). In the definition of the concurrence C, the eigenvalues are given in non-increasing order, such that λ1 ≥ λ2 ≥ λ3 ≥ λ4.
For a maximally entangled state, we have C = 1, and for a separable state, C = 030.
Therefore, considering the density matrix in Eq. (8), the concurrence of the system is obtained as
$$C=\max \left\{0,\frac{\sinh (2{{\mathcal{X}}})-\exp (-2{{\mathcal{X}}})}{\cosh (2{{\mathcal{X}}})+\exp (-2{{\mathcal{X}}})}\right\},$$
(15)
where, we define \({{\mathcal{X}}}=(a(t)/a({t}_{0}))({{\mathcal{A}}}/{k}_{B}{T}_{0})\).
The dependence of the concurrence on the hyperfine coupling expression in Eq. (2) and the scaling factor in Eq. (7) explicitly demonstrates that the expansion-induced entanglement can be expressed in terms of fundamental physical constants—the Boltzmann and Planck constants, the rest of masses of the electron and proton, Newton’s gravitational constant, the speed of light, as well as the elementary charge and the Bohr radius.
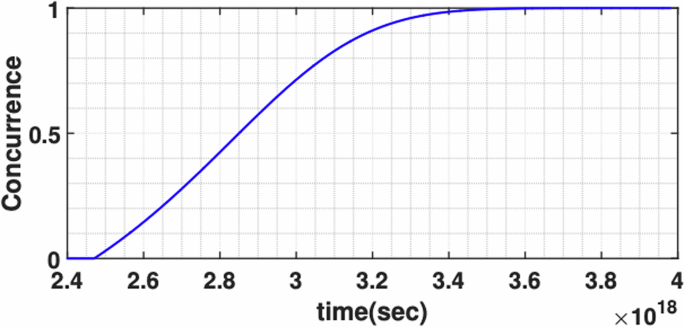
In Fig. 1, we present the dynamics of the concurrence in terms of the age of the universe. The results show that the unbounded neutral hydrogen atom’s concurrence is zero before the universe reaches an age of approximately 2.5 × 1018 seconds or 80 billion years, indicating the absence of entanglement until this point. However, at this critical time, hydrogen atoms begin to store quantum entanglement between their electrons and protons. This onset of entanglement is referred to as the quantum sudden birth phenomenon, which can be observed in some peculiar quantum systems31. In fact, the sudden birth along with the sudden death of entanglement are intriguing quantum features, emerging in certain physical systems31,32,33. This critical time, for the cosmic entanglement of sudden birth, can analytically be determined from the concurrence in Eq. (15), such that
$${t}_{c}=\frac{2}{3\sqrt{{\Omega }_{\Lambda }}{H}_{0}}{\sinh }^{-1}\left[{{\mathcal{R}}}\sinh \left(\frac{3}{2}\sqrt{{\Omega }_{\Lambda }}{H}_{0}{t}_{0}\right)\right],$$
(16)
where \({{\mathcal{R}}}={({k}_{B}{T}_{0}\ln 3/4{{\mathcal{A}}})}^{3/2}\). It is evident that this critical time depends on the current value of the cosmological parameters such as the universe’s age, dark energy density, Hubble parameter and CMB temperature, as well as the hyperfine structure constant of the hydrogen atom.
When the universe is about 2.5 × 1018 seconds old, the neutral hydrogens naturally start storing entanglement in their hyperfine structures. The entanglement reaches its maximum at the age of about 3.6 × 1018 seconds when all neutral hydrogen becomes maximally entangled.
To articulate the relationship between this critical time and the fundamental physical constants, we can express the parameter \({{\mathcal{R}}}\) as
$${{\mathcal{R}}}={\left(\frac{3\ln 3}{2}\frac{({k}_{B}{T}_{0}){a}_{0}^{2}}{{\alpha }^{2}{h}^{2}}\frac{{m}_{p}}{{g}_{e}{g}_{p}}\right)}^{3/2}={\left(\frac{3\ln 3}{4{\alpha }^{2}{g}_{e}{g}_{p}}\frac{{m}_{p}}{{m}_{e}}\frac{{k}_{B}{T}_{0}}{{E}_{0}}\right)}^{3/2},$$
where α is the fine-structure constant and E0 ≈ 13.6 eV is the binding energy (Bohr energy) of the ground-state of the hydrogen atom.
Applying the approximation \({\sinh }^{-1}(y)\approx \ln (2y)\), the critical time tc, can be simplified into
$${t}_{c}\approx \sqrt{\frac{3}{8\pi G{\rho }_{\Lambda }}}\ln \left(0.57\frac{{k}_{B}{T}_{0}}{{{\mathcal{A}}}}\right),$$
(17)
which explicitly depends on the Newton’s gravitational constant G and the dark energy density at the present time ρΛ.
An interesting feature of this entanglement sudden birth phenomenon is its emergence within the cosmological framework, highlighting an intricate interplay between quantum mechanics and the fabric of the cosmos. After this critical time, as time progresses, the entanglement steadily enhances with the universe’s age until it reaches its saturation point, where all unbounded neutral hydrogen atoms become maximally entangled. This saturation occurs when the universe is around 115 billion years old [see Fig. 1].
Equation (11) demonstrates the intimate connection between the quantum entanglement quantified by EOF and the von Neumann entropy of the system. The von Neumann entropy in a quantum system can relate the system’s disorder to the presence of quantum entanglement.
Therefore, to gain a deeper understanding of the entanglement entropy within the system, it is enlightening to examine the EOF of the system. For t ≥ tc, the closed-form analytical form of the EOF can be expressed as
$$E(\rho )={\log }_{2}\left[\left(\frac{2f}{\sqrt{{f}^{2}-1}}\right){\left(\frac{f+1}{f-1}\right)}^{\frac{1}{2f}}\right]$$
(18)
where, \(f=(\cosh (2{{\mathcal{X}}})+\exp (-2{{\mathcal{X}}}))/\sqrt{3}\).
Figure 2a depicts the time evolution of the EOF for the background hydrogen atoms. The correlation stored in the system is a result of the entanglement within the hyperfine structure of the atom. The plot shows that the entanglement of formation is zero before the threshold moment of the entanglement’s sudden birth. After this point, the EOF of the system starts to rise, reaching a maximum value at the saturation point. This can also be understood directly from Eq. (18), since E(ρ) approaches 1 as \({{\mathcal{X}}}\) approaches infinity. Therefore, depending on the density of neutral hydrogen, the universe undergoes a phase of increasing quantum correlation due to the birth of entanglement in neutral hydrogen atoms. This entanglement entropy is fundamentally different from the classical entropy in the cosmos and has a pure quantum mechanical origin. It is noteworthy that the link between entanglement and thermodynamic quantities34,35,36 may reveal new aspects of the expansion-induced entanglement developed here, prompting further intriguing considerations.
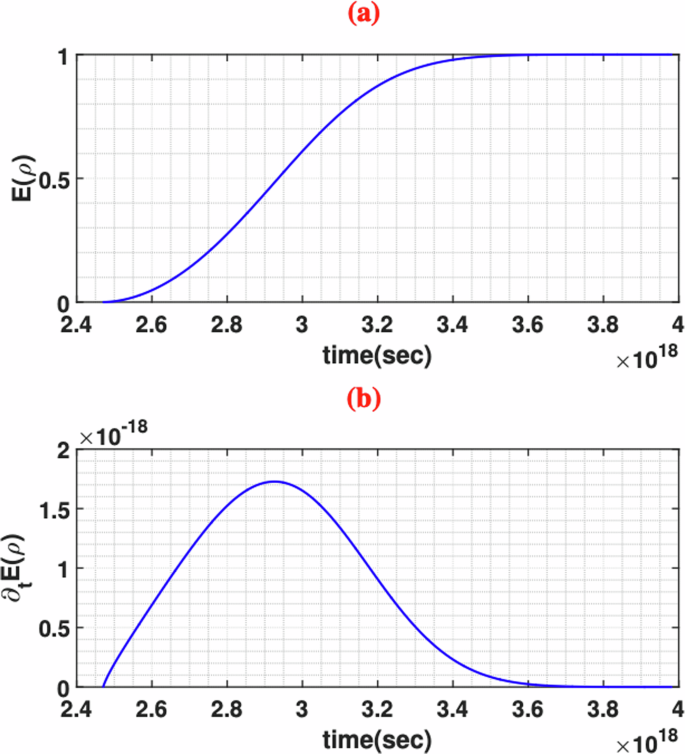
a EOF of the background hydrogen’s hyperfine structure as a function of time. When the universe is about 2.5 × 1018 seconds old, the EOF of neutral hydrogen naturally starts to enhance and finally reaches its maximum at the age of about 3.6 × 1018 seconds. b Entanglement production rate of the background hydrogen as a function of time. Once the buildup of entanglement is triggered, the entanglement production rate starts to increase, reaching its maximum value of approximately 1.7 × 10−18 s−1 when the universe is around 2.9 × 1018 seconds old. The production rate begins to decline after this age and approaches zero when the universe is roughly 115 billion years old.
As a valuable insight, we investigate the rate of EOF production in the background hydrogen atoms during the evolution of the universe. Figure 2b illustrates the time evolution of the entanglement production rate in the background neutral hydrogen atom. Once the buildup of entanglement is triggered, the entanglement production rate starts to increase, indicating a higher rate of entanglement buildup as time progresses. The production rate reaches its maximum value of approximately 1.7 × 10−18s−1 when the universe is around 2.9 × 1018 seconds old. Beyond this point, the production rate begins to decline and becomes vanishingly small when the universe is roughly 115 billion years old, indicating the saturation of entanglement storage.
It is noteworthy that, even though the intergalactic regions, in most cases, exhibit significantly lower matter density, due to the vast expanse of these regions, the proportion of baryonic matter in the intergalactic medium is comparable to the total matter content within galaxies (e.g., more than 80%37), including unbound hydrogen. Also, galaxies may feed their hydrogen to the intergalactic region through interactions with other gravitational sources. As mentioned earlier, the responsible phenomena for such processes may include ram pressure stripping3, turbulent viscous stripping3, and tidal stripping4,5. As one interesting process, stars within galaxies may contribute to the intergalactic medium by releasing their outer layers of hydrogen through stellar winds. This phenomenon is exemplified in the Cigar Galaxy (M82)38, where stellar winds expel matter from the galaxy into the surrounding space.
It is worth mentioning that this work deals with the entanglement of the unbound hydrogen atom within the cosmic background. However, the potential for observing entanglement extends to hydrogen gas systems when the temperature falls below the critical temperature for the entanglement’s sudden birth. According to current data on cold hydrogen gas systems, the lowest observed temperature is around 0.1 K in the Boomerang Nebula39, which still exceeds the required critical temperature for this entanglement emergence. Nonetheless, future observational endeavors may reveal cold hydrogen clouds with temperatures meeting the critical threshold, opening up exciting avenues for further exploration.
It is also important to note that the emergence of entanglement in the hydrogen atoms at sufficiently low temperatures can experimentally be explored with current technologies in the laboratory. Refrigeration systems at the mK level are readily available. Detection and quantification of entanglement can be achieved using established methods, including entanglement witness and density matrix tomography. The emergence of entanglement in sufficiently cold hydrogen atoms holds promise for laboratory exploration by creating experimental platforms that replicate the effects of the CMB temperature on atomic hydrogen.
Read our previous article: Ruthless Liverpool exploit everlasting flaws in Ange Postecoglou’s chaotic Tottenham
Sports Update: Therefore, the density matrix of the hyperfine structure can be expressed as \({\rho }_{ep}(t)=\frac{1}{z}{e}^{-\beta (t){h}_{hf}}\), where \(z=tr({e}^{-\beta (t){h}_{hf}})\) represents the partition function, and β(t) = 1/kbt(t) determines the background temperature at the age of the universe t.expressing the density matrix of the hydrogen atom explicitly in the basis \(\{\vert {\uparrow }_{e}{\uparrow }_{p}\rangle ,\vert {\uparrow }_{e}{\downarrow }_{p}\rangle ,\vert {\downarrow }_{e}{\uparrow }_{p}\rangle ,\vert {\downarrow }_{e}{\downarrow }_{p}\rangle \}\), the state of the system in thermal equilibrium with the cmb radiation is attained to be$${\rho }_{ep}(t)=\frac{1}{z}\left(\begin{array}{cccc}{e}^{-\beta (t){{\mathcal{a}}}}&0&0&0\\ 0&{{\mathcal{p}}}&{{\mathcal{q}}}&0\\ 0&{{\mathcal{q}}}&{{\mathcal{p}}}&0\\ 0&0&0&{e}^{-\beta (t){{\mathcal{a}}}}\\ \end{array}\right),$$ (8) where the matrix entries \({{\mathcal{p}}}\) and \({{\mathcal{q}}}\) are given by$${{\mathcal{p}}}=\frac{1}{2}({e}^{3\beta (t){{\mathcal{a}}}}+{e}^{-\beta (t){{\mathcal{a}}}})$$ (9) $${{\mathcal{q}}}=\frac{1}{2}({e}^{3\beta (t){{\mathcal{a}}}}-{e}^{-\beta (t){{\mathcal{a}}}})$$ (10) with this density matrix in hand, we can consider the entanglement in the hydrogen atom Stay tuned for more updates on Cosmic entanglement sudden birth: expansion-induced entanglement in hydrogen atoms and other trending sports news!
Your Thoughts Matter! What’s your opinion on Cosmic entanglement sudden birth: expansion-induced entanglement in hydrogen atoms? Share your thoughts in the comments below and join the discussion!